Regresión lineal.

La regresión lineal se utiliza cuando se cuenta con un conjunto de pares ordenados y se pretende obtener la ecuación de una recta que mejor se ajuste a esos puntos. Generalmente esta función que se obtiene se puede utilizar para estimar ciertos valores desconocidos. A continuación explicaré como obtener la ecuación de la recta de regresión.

Entonces supongamos que tenemos el siguiente conjunto de puntos o pares ordenados:

x	y
1	142,93
2	177,53
3	188,85
4	208,63
5	199,41
6	266,56
7	205,79
8	233,25
9	235,55
10	237,08
11	279,91
12	246,92
13	243,62
14	266,64
15	401,37
16	383,75
17	369,66
18	288,3
19	317,91
20	510,51

Cabe destacar que los valores  «y» del conjunto se han obtenidos experimentalmente.

Representados en un gráfico de dispersión queda de la siguiente forma:

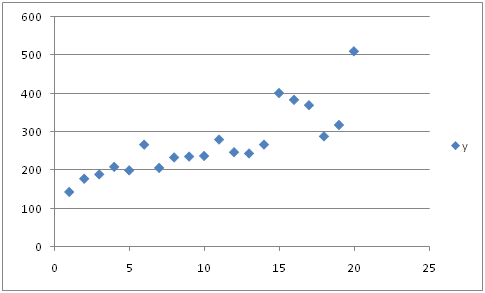
Entonces nuestra misión es encontrar una recta que se ajuste a esos valores, quedando de la siguiente manera:

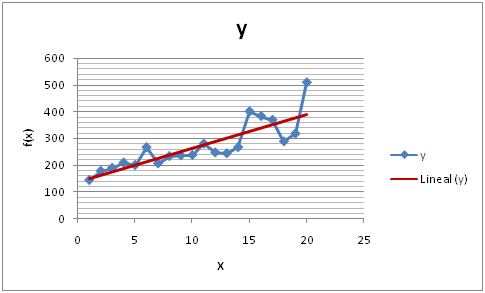
La recta roja, representa la MEJOR aproximación lineal de los puntos indicado con azul.

Como sabemos, la ecuación de una recta está dada de la siguiente manera:

f(x) = a x + b

Entonces nuestro objetivo es encontrar los valores de los coeficientes «a» y «b».

Dichos valores se pueden calcular de la siguiente forma utilizando el método de los mínimos cuadrados:
     

         

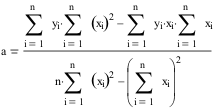
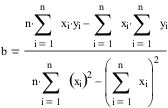
Realizando los cálculos correspondientes para los datos del ejemplo anterior tenemos que:

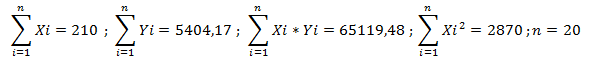
Entonces reemplazando los valores correspondientes en las fórmulas para obtener los coeficientes, tenemos los siguientes resultados:

a =  12,595

b = 137,96

Entonces la ecuación de la recta que estamos buscando es:

f(x) = 12,595x + 137,96

Entonces a partir de esta ecuación podemos estimar los valores de «x» que no conocemos.

Finalmente podemos indicar el resultado con el gráfico completo, incluyendo la ecuación de la recta:

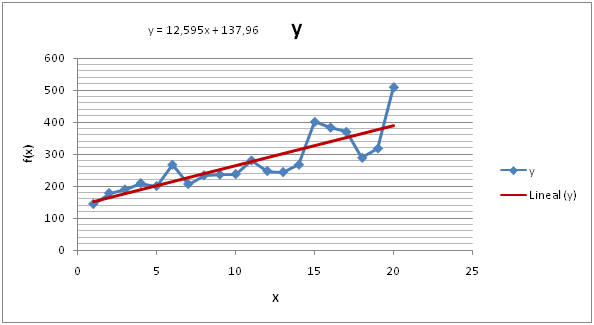
Espero que sea de utilidad.