Método Gauss Seidel

Este es uno de los métodos mas interesantes del análisis numérico y particualmente útil ya que nos permite encontrar la solución de un sistema de «n» ecuaciones con «n» incógnitas.

Para comenzar es preciso mencionar que es un método iterativo, es decir que debe aplicarse recursivamente hasta encontrar una solucion adecuada o con un error considerablemente pequeño.

En cada iteración obtenemos una solución posible del sistema con un error determinado, a medida que aplicamos nuevamente el método, la solución puede ser más precisa, entonces se dice que el sistema converge, pero si al aplicar el método reiteradas veces la solución tiene un error (ya explicaremos como se calcula este error) cada vez mayor se dice que el sistema no converge y no se puede resolver el sistema de ecuaciones por este método.

Bien proseguiré con la explicación del método y luego aclararé los detalles necesarios para determinar la eficacia del mismo.

Teniendo el siguiente sistema de ecuaciones:

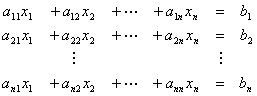
Despejamos x1 de la ecuación 1, x2 de la ecuación 2, … , xn de la ecuación n, quedando:

Desde la formula anterior resultan las fórmulas que se deberán ir aplicando en las diferentes iteraciones. Para comenzar a aplicar el método debemos asignar un valor arbitrario a las variables x2,…xn con el fin de obtener x1. Lo mas conveniente en este caso es que los valores comiencen en cero, lo cual nos facilitaría el trabajo ya que se reduce el cálculo de las primeras soluciones, entonces de esto resulta que:

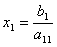
Ahora despejamos x2 de la ecuación 2 y reemplazamos a x1 por el valor obtenido en la ecuación anterior. De esto nos queda:

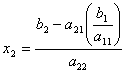
Una vez que tenemos x2, despejamos x3 de la ecuación 3 y así sucesivamente con las n ecuaciones, cada vez asignando el valor de las x1, x2, … xn-1 obtenido en el paso anterior.

Cuando hemos despejado las xn, tenemos lo que se conoce como primera solución o solución de la primer iteración:

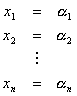
Con los nuevos valores de x1, x2,…,xn aplicamos los mismos pasos anteriores pero con los nuevos valores de las xn, de esta manera conseguimos una segunda solución:

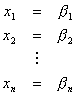
Al tener esta segunda solución estamos en condiciones de calcular el error que se calcula como sigue:

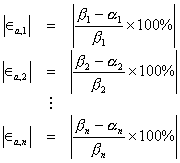
Así, repetimos el método tantas veces hasta que el error sea muy pequeño o los suficientemente aceptable.

Ahora solo queda mencionar que para que un sistema sea convergente se debe cumplir que la matriz de coeficientes sea diagonalmente dominante, y para ello se debe verificar la siguiente expresión:

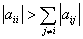
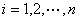
Si no se cumple esa condición, se puede permutar las filas de la matriz, con el fin de poder convertirla en una diagonalmente dominante.

Ahora mostraré un ejemplo, mediante el uso de un programa hecho en Visual Basic que hice para aplicar el método. El programa podrá ser descargado desde aqui. Para que todos los puedan ver y tratar de entender el funcionamiento del método.

Al iniciar el programa indico que la matriz de coeficientes es de 3 filas y 3 columnas (la matriz siempre tiene que ser cuadrada). Entonces supongamos los siguientes coeficientes:

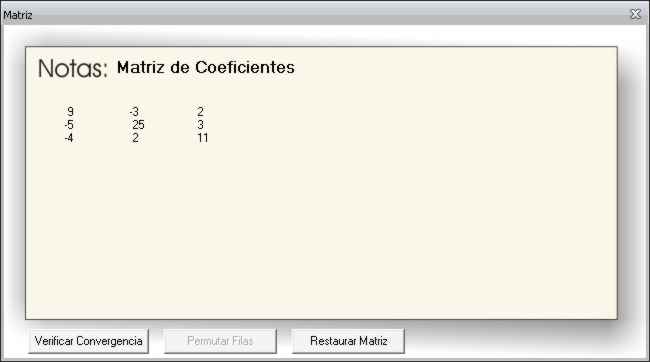
Luego cargo la matriz «b» que es la que contiene el valor de los resultados de las ecuaciones:

Hago clic en el botón verificar convergencia y si el programa me dice que se verifica, indico cuantas iteracciones quiero realizar y pulso en el botón «Calcular solución».

De esta forma el programa me arroja la solución del sistema (el valor de x1, x2,…xn) y me muestra el error, denominado por el programa como «Norma Infinito».

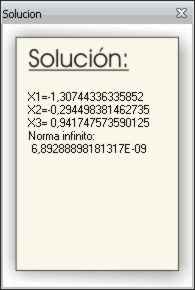
Se puede apreciar que la norma infinito no las muestra en notación científica, ya que es un error muy pequeño.

También el programa tiene la opción de guardar todas las iteracciones que hizo, hasta llegar a la ultima, esta opción es muy útil ya que se pude ver como fueron variando las soluciones hasta llegar a la última iteracción indicada, a medida que se hacen mas iteracciones, mas precisa es la solución.

Para finalizar, aquí muestro la secuencia que me arrojó el programa para este ejemplo:

Resolucion de Sistema de Ecuaciones Lineales
--------------------------------------------
Matriz A
--------
9 -3 2
-5 25 3
-4 2 11
Matriz B
--------
-9
2
15
--------------------------------------------
Solucion N°:1
------------

X1=-1
X2=-0,12
X3= 1,02181818181818
Norma Infinito: 1,02181818181818

——————————————–
Solucion N°:2
————

X1=-1,26707070707071
X2=-0,296032323232323
X3= 0,956707438016529
Norma Infinito: 0,267070707070707

——————————————–
Solucion N°:3
————

X1=-1,31127909397
X2=-0,297060711355984
X3= 0,940818640621087
Norma Infinito: 4,42083868992962E-02

——————————————–
Solucion N°:4
————

X1=-1,30809104614557
X2=-0,294516446103644
X3= 0,941515337056819
Norma Infinito: 3,18804782443349E-03

——————————————–
Solucion N°:5
————

X1=-1,30739777915829
X2=-0,294461396278475
X3= 0,941757425083982
Norma Infinito: 6,93266987283891E-04

——————————————–
Solucion N°:6
————

X1=-1,30743322655593
X2=-0,294497536321264
X3= 0,941751106038073
Norma Infinito: 3,61400427889014E-05

——————————————–
Solucion N°:7
————

X1=-1,30744386900444
X2=-0,294498906525456
X3= 0,941747485184833
Norma Infinito: 1,06424485053491E-05

——————————————–
Solucion N°:8
————

X1=-1,30744352110511
X2=-0,294498402443203
X3= 0,941747520042359
Norma Infinito: 5,04082253327542E-07

——————————————–
Solucion N°:9
————

X1=-1,30744336082381
X2=-0,294498374569846
X3= 0,941747573258585
Norma Infinito: 1,60281300898291E-07

——————————————–
Solucion N°:10
————

X1=-1,30744336335852
X2=-0,294498381462735
X3= 0,941747573590125
Norma Infinito: 6,89288898181317E-09

——————————————–

Descargar Programa Método Gauss Seidel

ModulosGaussSeidel