Análisis de nivelación en un proyecto empresario

A la hora de llevar adelante un proyecto empresario nos suelen surgir algunas preguntas tales como: Cual es el nivel mínimo de ventas que debe lograrse para que los costos o desembolsos sean recuperados, cual es el nivel mínimo de ventas para no operar con pérdidas, cual es el nivel de ventas para alcanzar las ganacias deseadas, cual será el incremento necesario en el nivel de ventas para contrarestar una disminucíon de precios, etc. Con éste análisis podemos tener respuestas aproximadas a todos estos interrogantes. Explicaré como llevar adelante dicho cálculo.

A fin de contestar temas como los indicados, necesitaremos conocer funciones como, por ejemplo:  las que nos indican el comportamiento del ingreso total (IT) y la del costo total (CT), que no requieren, en un análisis primario, ser muy ajustadas y, por lo tanto con funciones lineales es suficiente para el cometido expuesto.

Los costos totales pueden separarse en dos componentes: fijos y variables. Los costos fijos se mantienen constantes para todo el nivel del análisis. Es decir que se trabajará con una cantidad del producto que varía desde 0 hasta Xn, dentro del cual éstos serán constantes. Con respecto a los costos variables, diremos que fluctúan en función de la producción.

Supondremos: 

• Que los costos de los insumos (sus precios), no varían o sea, permanecen constantes. Nos referimos al precio de las materias primas, sueldos y jornales, etc. El análisis se hace para períodos acotados de tiempo: semanas, meses, años, etc.
• Que la eficiencia operativa, tanto de máquinas como de los operarios, no variará, como así tampoco la tecnología aplicada. Tendremos presente en este punto, que el análisis se efectuará con una determinada capacidad productiva total, que hará que tengamos un máximo de capacidad.
• Que los precios de venta no variarán para cualquier nivel de producción y ventas. De este modo gráficamente la función de ventas será una recta que nace desde el origen.
• Que la producción y la venta de la misma estén sincronizadas, es decir que la cantidad producida sea la vendida, no proviniendo el bien vendido de existencias de stock previos.

Ahora estableceremos las ecuaciones básicas del sistema expuesto. Luego lo plasmaremos en un gráfico a fin de poder visualizar mejor el tema.

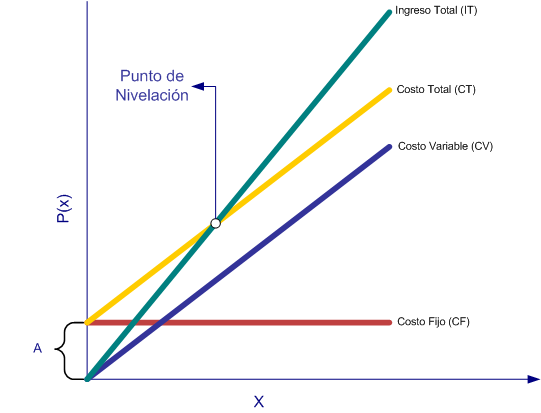
En lo gráfico utilizaremos un par de ejes cartesianos, en cuya ordenada ubicaremos los costos y los ingresos medidos en unidades monetarias, y en el eje de abscisas colocaremos la producción X, o bien las ventas V, según el análisis que efectuemos. Tendremos el siguiente sistema de ecuaciones:

• CV es el costo variable.
• CF es el costo fijo
• CT es el costo total

Donde el costo variable será CV = BX donde B, o sea el coeficiente angular, será el costo variable, y X será la producción o cantidad de producto. De tal modo tendremos (si usamos funciones lineales),  una recta que arranca desde el origen del par de ejes cartesianos.Es así, porque este tipo de costo varía en función de X, es decir de la producción.Si no producimos, no hay costo: es cero. Cuando comenzamos a producir, comienzan a existir costos variables.En cuanto al costo fijo, no será así, pues no depende de la producción, existiendo en forma independiente de ella, su expresión puede ser entonces: CF = A, donde A es un parámetro que nos indica su cuantía,  siendo su gráfica una recta que arrancará en el nivel pertinente de la ordenada.Por suma de funciones obtendré el costo total, o sea:CT = CF + CV = A + BX; o sea que naturalmente se adecua a lo dicho, la ecuación general de la recta.En cuanto al ingreso total, si como sabemos es una función de la producción (X), será: IT = XPx,  es decir: la cantidad del producto por su precio Px (que como hemos dicho, es constante). Con estas dos funciones tenemos un sistema de ecuaciones (en economía los sistemas de ecuaciones se denominan modelos), que es el siguiente:

 CT = A + BX

 IT   = XPx

  Nivelación en unidadesAnalíticamente, si queremos saber cual será el punto de nivelación necesario medido en unidades para cubrir  los gastos de producción totales, tenemos que conocer las ecuaciones del ingreso total y del costo total.Si adoptamos un sistema de funciones lineales, tendremos:

CT = A + BX

IT  = X.Px

En la intersección de ambas funciones, el punto común de las mismas constituye el denominado punto de nivelación y su valor en la abscisa Xn, será el número de unidades que se deberá vender a fin de cubrir el costo total. Luego, igualando ambas ecuaciones, tenemos: XPx = A + BX Por lo tanto luego de agrupar los términos en X,  sacarlo factor común y despejarlo, tendremos:

Xn = A/(Px – B)

Espero que les sea útil esta pequeña herramienta de análisis.

Saludos, Geroman. 😉